Parallélisme et Perpendicularité
Comprendre le Parallélisme et Perpendicularité
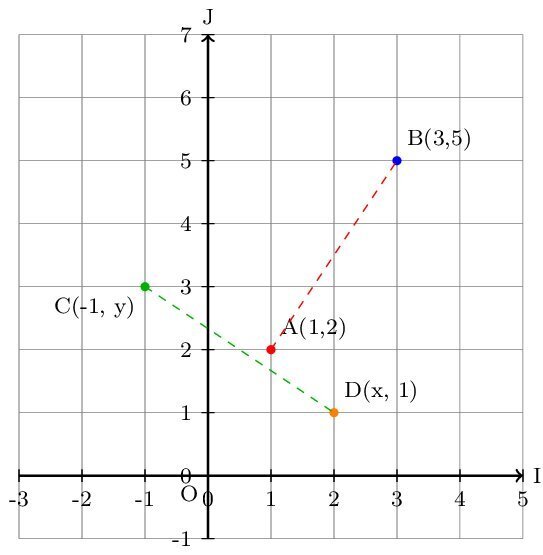
Dans un repère orthonormé \((O, I, J)\), On considère les points \(A(1, 2)\), \(B(3, 5)\), \(C(-1, y)\) et \(D(x, 1)\).
Partie A: Parallélisme
1. Calcul des coefficients directeurs :
- Déterminez le coefficient directeur de la droite \((AB)\).
- Exprimez le coefficient directeur de la droite \((CD)\) en fonction de \(y\).
2. Condition de parallélisme :
- Écrivez la condition pour que les droites \((AB)\) et \((CD)\) soient parallèles.
- Trouvez la valeur de \(y\) pour que \((AB)\) et \((CD)\) soient parallèles.
Partie B: Perpendicularité
1. Coefficient directeur de \((AD)\) :
- Exprimez le coefficient directeur de la droite \((AD)\) en fonction de \(x\).
2. Condition de perpendicularité :
- Écrivez la condition pour que les droites \((AB)\) et \((AD)\) soient perpendiculaires.
- Résolvez cette condition pour trouver la valeur de \(x\).
Partie C: Application et vérification
- Avec les valeurs de \(x\) et \(y\) trouvées, vérifiez si le quadrilatère formé par les points \(A\), \(B\), \(C\), et \(D\) a des côtés opposés qui sont à la fois parallèles et perpendiculaires.
- Calculez les distances \(AB\) et \(CD\) pour vérifier si elles sont égales, ce qui pourrait indiquer que \(ABCD\) est un rectangle ou un parallélogramme particulier.
Correction : Parallélisme et Perpendicularité
Partie A: Parallélisme
1. Calcul des coefficients directeurs:
a) Droite AB
Pour deux points \( (x_1,y_1) \) et \( (x_2,y_2) \), le coefficient directeur est défini par
\[m = \frac{y_2 – y_1}{x_2 – x_1}.\]
Pour \( A(1,2) \) et \( B(3,5) \) :
\[m_{AB} = \frac{5 – 2}{3 – 1} = \frac{3}{2}.\]
b) Droite CD
La droite passant par \( C(-1,y) \) et \( D(x,1) \) possède pour coefficient directeur :
\[m_{CD} = \frac{1 – y}{x – (-1)} = \frac{1 – y}{x + 1}.\]
À ce stade, \( m_{CD} \) est exprimé en fonction de \( y \) (et de \( x \)).
2. Condition de parallélisme
Deux droites sont parallèles si et seulement si elles ont le même coefficient directeur.
Ainsi, on impose :
\[m_{AB} = m_{CD}.\]
En substituant les expressions obtenues :
\[\frac{3}{2} = \frac{1 – y}{x + 1}.\]
Nous retiendrons cette équation afin de déterminer \( y \) une fois que nous connaîtrons \( x \).
Partie B : Perpendicularité
1. Coefficient directeur de la droite \((AD)\)
La droite \((AD)\) passe par \( A(1,2) \) et \( D(x,1) \). Son coefficient directeur est :
\[m_{AD} = \frac{1 – 2}{x – 1} = \frac{-1}{x – 1}.\]
2. Condition de perpendicularité entre \((AB)\) et \((AD)\)
Deux droites sont perpendiculaires si le produit de leurs coefficients directeurs est égal à \(-1\).
On impose donc :
\[m_{AB} \times m_{AD} = -1.\]
Nous connaissons \( m_{AB} = \frac{3}{2} \) et \( m_{AD} = \frac{-1}{x – 1} \).
Ainsi :
\[\frac{3}{2} \times \frac{-1}{x – 1} = -1.\]
Détaillons la résolution :
- Multiplions :
\[\frac{-3}{2(x – 1)} = -1.\]
- Pour se débarrasser du dénominateur, multiplions les deux côtés par \( 2(x-1) \) :
\[-3 = -2(x – 1).\]
- En multipliant par \(-1\) pour simplifier :
\[3 = 2(x – 1).\]
- Résolvons pour \( x \) :
\[x – 1 = \frac{3}{2} \quad \Longrightarrow \quad x = 1 + \frac{3}{2} = \frac{2}{2} + \frac{3}{2} = \frac{5}{2}.\]
- Nous obtenons ainsi :
\[{x = \frac{5}{2}}.\]
Retour à la Partie A : Détermination de \( y \)
Nous avions établi la condition de parallélisme :
\[\frac{3}{2} = \frac{1 – y}{x + 1}.\]
Nous venons de trouver \( x = \frac{5}{2} \). Calculons alors \( x + 1 \) :
\[x + 1 = \frac{5}{2} + 1 = \frac{5}{2} + \frac{2}{2} = \frac{7}{2}.\]
L’équation devient :
\[\frac{3}{2} = \frac{1 – y}{\frac{7}{2}}.\]
Pour simplifier, remarquez que diviser par \(\frac{7}{2}\) revient à multiplier par \(\frac{2}{7}\) :
\[\frac{3}{2} = \frac{2(1 – y)}{7}.\]
Résolvons maintenant cette équation pour trouver y :
- Multiplions des deux côtés par 7 :
\[\frac{3 \times 7}{2} = 2(1 – y) \quad \Longrightarrow \quad \frac{21}{2} = 2(1 – y).\] - Divisons par 2 :
\[1 – y = \frac{21}{4}.\] - Isolons \( y \) :
\[y = 1 – \frac{21}{4} = \frac{4}{4} – \frac{21}{4} = -\frac{17}{4}.\]
Nous obtenons ainsi :
\[{y = -\frac{17}{4}}.\]
Partie C : Application et vérification
1. Les coordonnées finales
Les points sont donc :
\[A(1,2), \quad B(3,5), \quad C\left(-1,-\frac{17}{4}\right), \quad D\left(\frac{5}{2},1\right).\]
2. Vérification des conditions de parallélisme et de perpendicularité
a) Parallélisme de \((AB)\) et \((CD)\)
Pour \((AB)\), nous avons déjà :
Pour \((CD)\), en utilisant \( C\left(-1,-\frac{17}{4}\right) \) et \( D\left(\frac{5}{2},1\right) \) :
Le numérateur :
\[1 – \left(-\frac{17}{4}\right) = 1 + \frac{17}{4} = \frac{4}{4} + \frac{17}{4} = \frac{21}{4}.\]
Le dénominateur :
\[\frac{5}{2} – (-1) = \frac{5}{2} + 1 = \frac{5}{2} + \frac{2}{2} = \frac{7}{2}.\]
Donc :
\[m_{CD} = \frac{\frac{21}{4}}{\frac{7}{2}} = \frac{21}{4} \times \frac{2}{7} = \frac{42}{28} = \frac{3}{2}.\]
On constate que :
\[m_{AB} = m_{CD} = \frac{3}{2},\]
Ce qui confirme que AB et CD sont parallèles.
b) Perpendicularité entre \((AB)\) et \((AD)\)
Pour \((AD)\), de \( A(1,2) \) à \( D\left(\frac{5}{2},1\right) \) :
\[m_{AD} = \frac{1 – 2}{\frac{5}{2} – 1}
\[m_{AD} =\frac{-1}{\frac{5}{2} – \frac{2}{2}}\]
\[m_{AD} = \frac{-1}{\frac{3}{2}} = -\frac{2}{3}.\]
Le produit :
\[m_{AB} \times m_{AD} = \frac{3}{2} \times \left(-\frac{2}{3}\right) = -1.\]
Le produit étant égal à \(-1\), cela confirme que \((AB)\) et \((AD)\) sont perpendiculaires.
3. Calcul des distances pour comparer les côtés opposés
a) Distance \( AB \)
Entre \( A(1,2) \) et \( B(3,5) \) :
\[AB = \sqrt{(3 – 1)^2 + (5 – 2)^2}\]
\[AB =\sqrt{2^2 + 3^2} \]
\[AB = \sqrt{4 + 9} = \sqrt{13}.\]
b) Distance \( CD \)
Entre \( C\left(-1,-\frac{17}{4}\right) \) et \( D\left(\frac{5}{2},1\right) \) :
- Calcul de la différence en abscisses :
\[x_D – x_C = \frac{5}{2} – (-1)\]
\[x_D – x_C = \frac{5}{2} + 1 \]
\[x_D – x_C = \frac{5}{2} + \frac{2}{2} = \frac{7}{2}.\]
- Calcul de la différence en ordonnées :
\[y_D – y_C = 1 – \left(-\frac{17}{4}\right)\]
\[y_D – y_C= 1 + \frac{17}{4}\]
\[y_D – y_C= \frac{4}{4} + \frac{17}{4} = \frac{21}{4}.\]
c) Distance \( CD \) :
\[CD = \sqrt{\left(\frac{7}{2}\right)^2 + \left(\frac{21}{4}\right)^2}\]
\[CD= \sqrt{\frac{49}{4} + \frac{441}{16}}.\]
Pour additionner, mettons \(\frac{49}{4}\) sur le dénominateur 16 :
\[\frac{49}{4} = \frac{49 \times 4}{16} = \frac{196}{16}.\]
Ainsi :
\[CD = \sqrt{\frac{196 + 441}{16}}\]
\[CD= \sqrt{\frac{637}{16}}\]
\[CD = \frac{\sqrt{637}}{4}.\]
On remarque que \( 637 = 49 \times 13 \), donc :
\[\sqrt{637} = \sqrt{49 \times 13} = 7\sqrt{13}.\]
Finalement :
\[CD = \frac{7\sqrt{13}}{4}.\]
d) Comparaison
Nous obtenons :
- \(AB = \sqrt{13} = \frac{4\sqrt{13}}{4},\)
- \(CD = \frac{7\sqrt{13}}{4}.\)
Comme \(\frac{7\sqrt{13}}{4} \neq \frac{4\sqrt{13}}{4}\), on conclut que \( AB \neq CD \).
Conclusion sur la nature du quadrilatère
-
Parallélisme :
La droite \((AB)\) est parallèle à la droite \((CD)\) car \( m_{AB} = m_{CD} = \frac{3}{2} \).
-
Perpendicularité :
La droite \((AD)\) est perpendiculaire à \((AB)\) puisque \( m_{AB} \times m_{AD} = -1 \).
-
Côtés opposés :
Pour qu’un quadrilatère soit un rectangle, il faut que :
Les deux paires de côtés opposés soient parallèles. Les angles doivent être droits (ce qui implique en particulier que les longueurs des côtés opposés soient égales dans un rectangle).
Ici, seule la paire \((AB)\) et \((CD)\) est parallèle, mais la seconde paire \((AD)\) et \((BC)\) n’est pas étudiée et, d’après le calcul de \( AB \) et \( CD \), les longueurs ne sont pas égales (\( AB = \sqrt{13} \) et \( CD = \frac{7\sqrt{13}}{4} \)). On peut donc conclure que le quadrilatère n’est ni un rectangle ni un parallélogramme complet.
Résumé des résultats
- Coefficient directeur de \((AB)\) :
\[m_{AB} = \frac{3}{2}.\] - Coefficient directeur de \((CD)\) (en fonction de \( y \) et \( x \)) :}
\[m_{CD} = \frac{1 – y}{x + 1}.\] - Condition de parallélisme \((AB) \parallel (CD)\) donne (après substitution de \( x = \frac{5}{2} \)) :
\[y = -\frac{17}{4}.\] - Coefficient directeur de \((AD)\) :}
\[m_{AD} = \frac{-1}{x – 1}.\] - Condition de perpendicularité \((AB) \perp (AD)\) donne :
\[x = \frac{5}{2}.\] - Distances :
\[AB = \sqrt{13} \quad \text{et} \quad CD = \frac{7\sqrt{13}}{4}.\]
Le quadrilatère défini par \( A(1,2) \), \( B(3,5) \), \( C\left(-1,-\frac{17}{4}\right) \) et \( D\left(\frac{5}{2},1\right) \) possède une paire de côtés opposés parallèles \((AB) \parallel (CD)\) et un angle droit en \( A \) (car \((AB) \perp (AD)\)).
Cependant, puisque la seconde paire de côtés opposés n’est pas parallèle et que les longueurs \( AB \) et \( CD \) diffèrent, ce quadrilatère n’est ni un rectangle ni un parallélogramme particulier.
Réponse finale :
\[{x = \frac{5}{2} \quad \text{et} \quad y = -\frac{17}{4}}\]
Le quadrilatère n’est pas un rectangle (les côtés opposés ne sont pas tous parallèles et \( AB \neq CD \)).
Parallélisme et Perpendicularité
D’autres exercices de géometrie première:

0 commentaires