Étude d’une fonction Linéaire

Comprendre l’Étude d’une fonction Linéaire

Soit la fonction linéaire \(f\) définie par

\[ f(x) = 3x – 5 \]

1. Représentation graphique

• Tracez la représentation graphique de la fonction \(f\) dans un repère orthogonal.

2. Calculs d’images

• Calculez \(f(0)\), \(f(2)\) et \(f(-1)\).

3. Calcul d’antécédents

• Déterminez un antécédent de \(4\) par \(f\).
• Existe-t-il plusieurs antécédents de \(4\) ? Justifiez votre réponse.

4. Interprétation géométrique

• Quel est le coefficient directeur de la droite représentant la fonction \(f\) ? Quelle est son interprétation géométrique ?
• Déterminez l’ordonnée à l’origine de cette droite.

5. Résolution d’équation

• Résolvez l’équation \(f(x) = 0\).

6. Comparaison de fonctions

• Considérons une seconde fonction linéaire \(g\) définie par \(g(x) = -\frac{1}{2}x + 3\). Sans tracer la représentation graphique de \(g\), comparez les pentes de \(f\) et \(g\). Quelle conclusion pouvez-vous tirer sur les directions des droites représentant \(f\) et \(g\) dans le même repère ?

Correction : Étude d’une fonction Linéaire

1. Représentation graphique

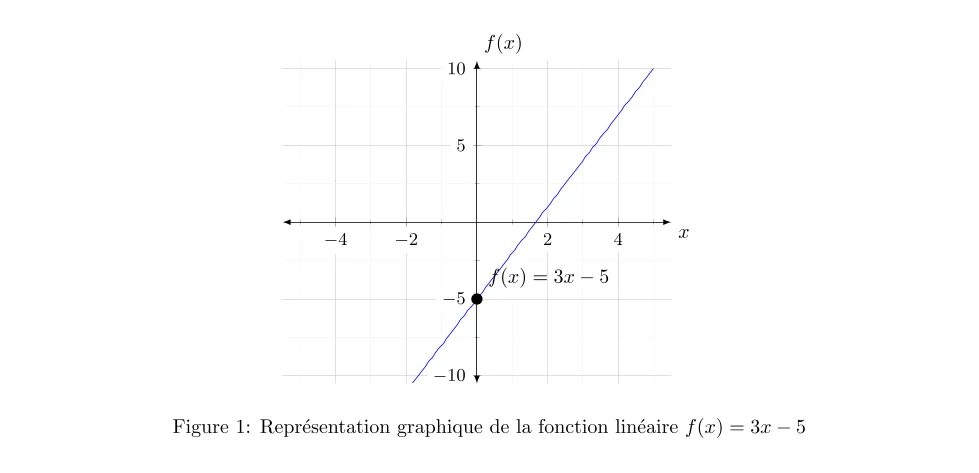
La fonction linéaire \(f(x) = 3x – 5\) se représente par une droite dans un repère orthogonal. Cette droite a un coefficient directeur (pente) de \(3\) et coupe l’ordonnée à \(-5\).

2. Calculs d’images

Pour calculer les images de certains nombres par la fonction \(f\), on substitue ces nombres dans l’expression de \(f(x)\).

Pour \(x = 0\):

\[ f(0) = 3 \times 0 – 5 = -5 \] L’image de \(0\) par \(f\) est \(-5\).

Pour \(x = 2\):

\[ f(2) = 3 \times 2 – 5 = 6 – 5 = 1 \] L’image de \(2\) par \(f\) est \(1\).

Pour \(x = -1\):

\[ f(-1) = 3 \times (-1) – 5 = -3 – 5 = -8 \] L’image de \(-1\) par \(f\) est \(-8\).

3. Calcul d’antécédents

Pour trouver un antécédent de \(4\) par la fonction \(f\), nous résolvons l’équation \(f(x) = 4\).

\[ 3x – 5 = 4 \] \[ 3x = 4 + 5 \] \[ 3x = 9 \] \[ x = \frac{9}{3} = 3 \]

L’antécédent de \(4\) par \(f\) est donc \(3\). Il n’existe qu’un seul antécédent de \(4\) par \(f\) car les fonctions linéaires sont bijectives sur \(\mathbb{R}\), ce qui signifie que chaque élément de l’ensemble d’arrivée a un unique antécédent.

4. Interprétation géométrique

• Le coefficient directeur de la droite représentant la fonction \(f\) est \(3\). Cela signifie que pour chaque unité que l’on se déplace horizontalement, la droite monte de \(3\) unités verticalement.
• L’ordonnée à l’origine est \(-5\), indiquant que le point où la droite intersecte l’axe des ordonnées est \((0, -5)\).

5. Résolution d’équation

Pour résoudre \(f(x) = 0\), on cherche le \(x\) pour lequel l’image par \(f\) est \(0\).

\[ 3x – 5 = 0 \] \[ 3x = 5 \] \[ x = \frac{5}{3} \approx 1.67 \]

La solution de l’équation \(f(x) = 0\) est environ \(1.67\), ce qui signifie que le point \((1.67, 0)\) est le point d’intersection de la droite avec l’axe des abscisses.

6. Comparaison de fonctions

La fonction \(f(x) = 3x – 5\) a une pente de \(3\), tandis que la fonction \(g(x) = -\frac{1}{2}x + 3\) a une pente de \(-\frac{1}{2}\).

Les pentes étant de signes opposés, les directions des droites sont également opposées : la droite de \(f\) monte tandis que celle de \(g\) descend.

Étude d’une fonction Linéaire