Planification de dépenses suite arithmétique

Comprendre la Planification de dépenses suite arithmétique

Marie gère un budget pour un projet sur 12 mois. Elle prévoit d’allouer une somme d’argent chaque mois pour ce projet, de manière à augmenter le montant alloué chaque mois de 200€ par rapport au mois précédent. Au premier mois, elle compte allouer 500€.

Questions:

1. Terme Général de la Suite:

• Exprimez le montant \(M_n\) alloué au n-ième mois sous forme d’une suite arithmétique. Identifiez le premier terme \(a\) et la raison \(r\).

2. Calcul du 12ème Terme:

• Calculez le montant que Marie allouera au 12ème mois.

3. Somme des Dépenses:

• Calculez la somme totale \(S\) que Marie aura dépensée à la fin des 12 mois.

4. Représentation Graphique:

• Proposez une représentation graphique de la suite \(M_n\) pour les 12 premiers mois.

5. Réflexion sur le Budget:

• Si Marie a un budget total de 10 000€ pour l’année, déterminera-t-elle que son plan est réalisable? Justifiez votre réponse en calculant si la somme totale des dépenses dépasse ou non ce budget.

Correction : Planification de dépenses suite arithmétique

1. Terme Général de la Suite

Définition:

La suite définie par le montant \(M_n\) alloué au n-ième mois est une suite arithmétique où le premier terme \(a\) est le montant initial alloué, soit 500 €, et la raison \(r\), qui est l’augmentation mensuelle, est de 200 €.

Formule du terme général d’une suite arithmétique:

\[ M_n = a + (n-1)r \]

Application:

\[ M_n = 500 + (n-1) \times 200 \]

2. Calcul du 12ème Terme

Utilisation de la formule du terme général:

\[ M_{12} = 500 + (12-1) \times 200 \] \[ M_{12} = 500 + 11 \times 200 \] \[ M_{12} = 500 + 2200 \] \[ M_{12} = 2700 \]

Donc, le montant alloué au 12ème mois est de 2700 €.

3. Somme des Dépenses

Formule de la somme des n premiers termes d’une suite arithmétique:

\[ S_n = \frac{n}{2} (a + M_n) \]

Calcul avec les valeurs de l’exercice:

\[ S_{12} = \frac{12}{2} (500 + 2700) \] \[ S_{12} = 6 \times 3200 \] \[ S_{12} = 19200 \]

La somme totale dépensée à la fin des 12 mois est de 19200 €.

4. Représentation Graphique

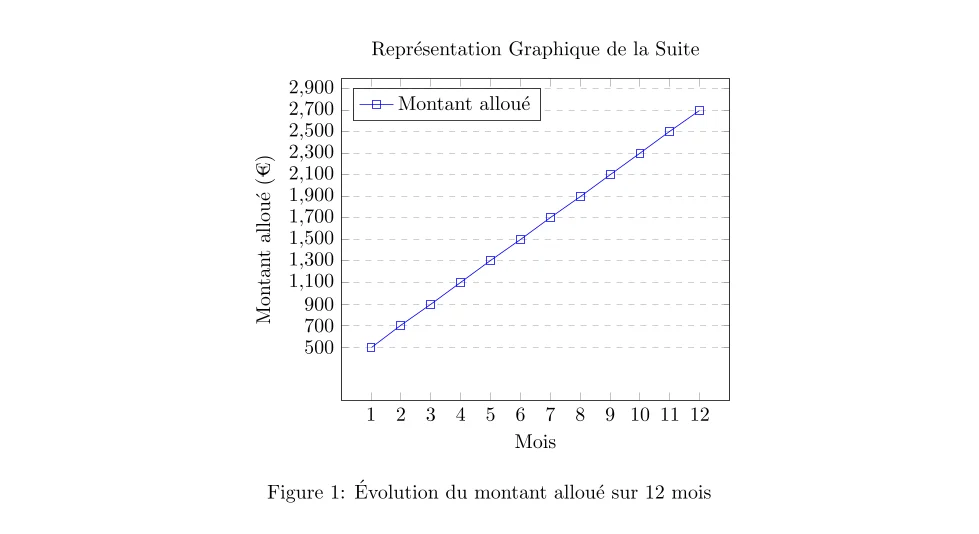
La suite peut être représentée graphiquement par une série de points alignés qui forment une ligne droite ascendante. L’axe horizontal (axe des abscisses) représente les mois (de 1 à 12), tandis que l’axe vertical (axe des ordonnées) représente le montant alloué chaque mois. Chaque point sur le graphique correspond au montant alloué pour un mois donné, commençant à 500 € et augmentant de 200 € chaque mois.

5. Réflexion sur le Budget

Analyse:

Pour déterminer si le plan est réalisable avec un budget total de 10 000 €, comparez ce budget à la somme totale des dépenses calculée.

Comparaison:

\[ S_{12} = 19200\,€ > 10\,000\,€ \]

Conclusion:

Le budget total de 10 000 € est insuffisant pour couvrir les dépenses planifiées de 19 200 €. Marie devra réajuster son plan budgétaire, soit en réduisant le montant initial alloué, soit en diminuant l’augmentation mensuelle, pour s’assurer que la somme totale des dépenses n’excède pas son budget disponible.

Planification de dépenses suite arithmétique