Analyse d’une figure composite

Comprendre l’Analyse d’une figure composite

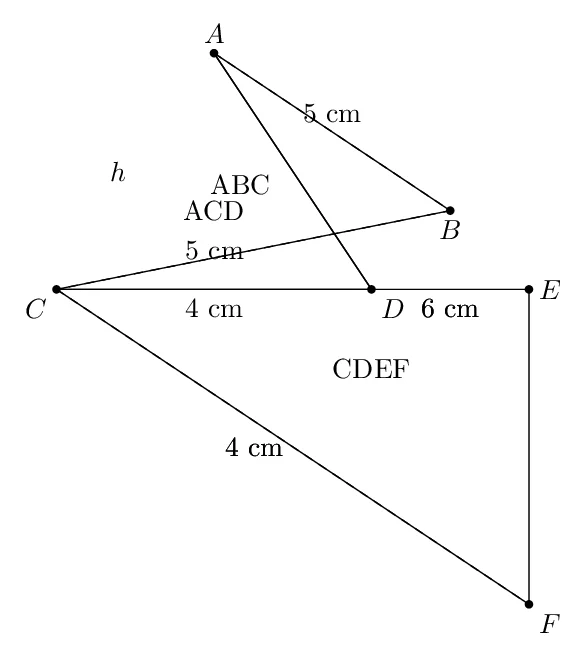
La figure ci-dessous est composée de deux triangles isocèles \(ABC\) et \(ACD\) (où \(AC\) est la base commune) et d’un rectangle \(CDEF\).

Le point \(A\) est situé au-dessus de \(C\) et \(D\) est à droite de \(C\). Les points \(E\) et \(F\) sont respectivement à droite de \(D\) et en dessous de \(C\), formant ainsi le rectangle \(CDEF\). Les mesures suivantes sont données :

• \(AC = CD = 4\) cm,
• \(AB = BC = 5\) cm,
• \(DE = 6\) cm,
• \(EF = 4\) cm.

Questions :

1. Calcul de l’aire des triangles \(ABC\) et \(ACD\) :

• Utilisez la formule de l’aire d’un triangle \((\text{base} \times \text{hauteur}) / 2\) pour calculer l’aire de chaque triangle. Pour \(ABC\), utilisez \(AC\) comme base et pour \(ACD\), utilisez \(CD\) comme base. La hauteur de ces triangles est la même et peut être trouvée en appliquant le théorème de Pythagore dans l’un des triangles isocèles.

2. Calcul de l’aire du rectangle \(CDEF\) :

• L’aire d’un rectangle est donnée par \(\text{longueur} \times \text{largeur}\). Utilisez les dimensions données pour calculer l’aire de \(CDEF\).

3. Calcul du périmètre de la figure composite :

• Le périmètre est la somme de toutes les longueurs des côtés extérieurs de la figure. Pour cela, n’oubliez pas que les côtés \(AC\) et \(CD\) sont partagés entre les triangles et le rectangle, donc ils ne sont comptés qu’une seule fois.

4. Démonstration que le triangle \(ABC\) est isocèle :

• Utilisez les propriétés des triangles isocèles pour justifier pourquoi \(ABC\) est isocèle en se basant sur les longueurs des côtés données.

5. Discussion sur la relation entre les triangles \(ABC\) et \(ACD\) :

Réfléchissez à la manière dont ces deux triangles sont liés entre eux et avec le rectangle \(CDEF\), notamment en termes de symétrie et de proportions.

Correction : Analyse d’une figure composite

1. Calcul de l’aire des triangles \(ABC\) et \(ACD\)

Pour calculer l’aire des triangles, nous avons besoin de leur base et de leur hauteur. La base des deux triangles est donnée (4 cm pour chacun).

Pour trouver la hauteur, nous appliquons le théorème de Pythagore dans le triangle \(ABC\) (qui est également valable pour \(ACD\) car ils sont isocèles et partagent la même base).

Triangle \(ABC\)

La hauteur \(h\) du triangle \(ABC\) est telle que :

\[ h^2 + \left(\frac{AC}{2}\right)^2 = AB^2 \] \[ h^2 + 2^2 = 5^2 \] \[ h^2 + 4 = 25 \] \[ h^2 = 21 \]
\[ h = \sqrt{21} \text{ cm} \]

Aire du triangle \(ABC\) :

\[\text{Aire}_{ABC} = \frac{\text{base} \times \text{hauteur}}{2} \] \[\text{Aire}_{ABC} = \frac{4 \times \sqrt{21}}{2} \] \[\text{Aire}_{ABC} = 2\sqrt{21} \text{ cm}^2\]

Triangle \(ACD\)

L’aire du triangle \(ACD\) est identique à celle du triangle \(ABC\) car ils ont la même base et la même hauteur.

\[\text{Aire}_{ACD} = 2\sqrt{21} \text{ cm}^2\]

2. Calcul de l’aire du rectangle \(CDEF\)

Pour calculer l’aire du rectangle \(CDEF\), nous utilisons la formule de l’aire d’un rectangle, qui est le produit de sa longueur par sa largeur. Les dimensions fournies pour \(DE\) et \(EF\) sont :

• \(DE = 6\) cm (la longueur),
• \(EF = 4\) cm (la largeur).

Donc, l’aire du rectangle \(CDEF\) est :

\[Aire_{CDEF} = DE \times EF \] \[Aire_{CDEF} = 6 \times 4 \] \[Aire_{CDEF} = 24 \text{ cm}^2\]

3. Calcul du périmètre de la figure composite

Pour calculer le périmètre de la figure composite, nous devons additionner les longueurs de tous les côtés extérieurs.

Le périmètre total devrait donc prendre en compte :

• Les côtés \(AB\) et \(BC\) (deux fois chaque pour les triangles),
• Les côtés \(AD\) et \(DC\) (uniquement \(DC\) car \(AD\) est superposé avec \(BC\)),
• Les longueurs \(DE\) et \(EF\), et enfin \(CF\), qui est égal à \(EF\).

Puisque \(AD = BC = 5\) cm (triangle isocèle \(ABC\)) et \(DC = AC = 4\) cm, le calcul du périmètre est :

\[Périmètre = AB + BC + DC + DE + EF + CF \] \[Périmètre = 5 + 5 + 4 + 6 + 4 + 4 \] \[Périmètre = 28 \text{ cm}\]

4. Démonstration que le triangle \(ABC\) est isocèle

Le triangle \(ABC\) est isocèle car il a deux côtés de même longueur : \(AB = BC = 5\) cm, ce qui est une caractéristique définissant les triangles isocèles.

5. Discussion sur la relation entre les triangles \(ABC\) et \(ACD\), et le rectangle \(CDEF\)

Les triangles \(ABC\) et \(ACD\) partagent une base commune \(AC\) et sont donc symétriques l’un par rapport à l’autre autour de cette base.

Le rectangle \(CDEF\), attaché à la base \(CD\) du triangle \(ACD\), complète la figure en formant une structure composite où les propriétés des figures géométriques de base sont mises en évidence, offrant un bel exemple d’intégration de la géométrie plane dans une figure plus complexe.

Analyse d’une figure composite